2진법과 10진법
우리는 일상생활에서 주로 10진법을 사용한다. 1946년에 개발된 컴퓨터 에니악은 사람에게 익숙한 10진법을 사용하도록 설계되었지만, 전기 회로는 전압이 불안정하여 전압을 10단계로 나누어 처리하는 데 한계가 있었다.
그래서 1950년에 개발된 에드박은 단 두가지 단계, 전기가 흐르면 1, 전기가 흐르지 않으면 0으로만 동작하도록 설계되었고 매우 성공적이었기에, 지금까지 대부분의 컴퓨터는 2진법을 사용한다.

우리는 변수에 값을 저장하면 10진수로 저장되는 것처럼 보았지만, 실제로 컴퓨터는 2진수 밖에 모르기에, 2진수로 바뀌어 저장하게 된다.
따라서 age에 22를 저장하면 실제로는 2진수인 11001로 저장이 되는 것이다.
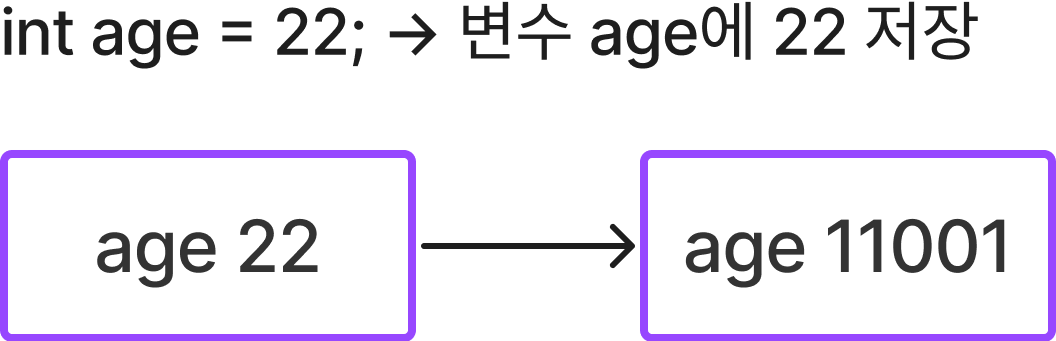
2진수는 0과 1로만 데이터를 표현하기에 10진수보다 많은 자리수를 필요로 하지만, 10진수를 온전하게 표현 할 수 있고, 연산도 할 수 있다.
비트(bit)와 바이트(byte)
한 자리의 2진수를 비트라고 하며, 1 비트는 컴퓨터가 값을 저장할 수 있는 최소단위다.
하지만 비트는 너무 작은 단위이기에 1 비트 8개를 묶어서 바이트로 정의해 데이터의 기본 단위로 사용한다.

워드(word)
비트와 바이트가 아닌 워드(word)라는 단위가 있다.
워드는 CPU가 한 번에 처리할 수 있는 데이터의 크기를 의미하며, 워드의 크기는 CPU의 성능에 따라 달라진다.
32비트 CPU에서 1 워드는 32 비트(4 바이트)이고, 64 비트 CPU에서 1 워드는 64 비트(8 바이트)이다.
8진법과 16진법
2진법은 0과 1로 값을 표현하기에 자리수가 매우 길어진다는 단점이 있기에, 8진법과 16진법을 사용한다.
8진수는 2진수 3자리를, 16진수는 2진수 4자리를 각각 한 자리로 표현할 수 있기에, 자리수가 짧아져서 가독성이 좋고, 서로 간의 변환 방법도 매우 간단하다.

2진수 -> 8진수, 16진수 변환
2진수에서 8진수는 뒷자리부터, 3자리씩 끊어서 해당 되는 8진수로 변경한다.
2진수에서 16진수는 3자리가 아닌 4자리씩 끊어서 해당 되는 16진수로 변경한다.

정수와 실수의 진법 변환
1. 10진수 -> N진수
10진수를 해당 진수로 나누고, 몫과 나머지는 아래부터 끝까지 반복하고 아래부터 위까지 순서대로 적으면 된다.

2. N진수 -> 10진수
각 자리의 수에 해당 단위의 값을 곱해서 모두 더한다.
아래의 예시는 2진수 1011를 10진수로 변환하는 과정이다.
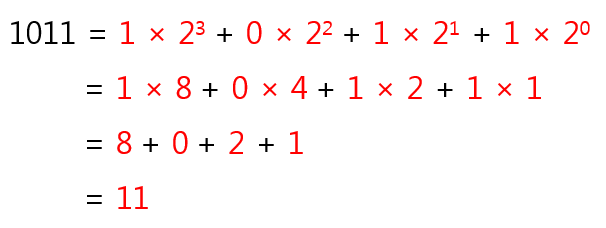
'CS > 자료구조' 카테고리의 다른 글
| Observer Pattern (1) | 2024.06.02 |
|---|---|
| 상대 패턴(State Pattern) (0) | 2024.04.13 |
| [자료 구조] Queue (0) | 2022.11.16 |
| [자료 구조] Stack (0) | 2022.11.16 |
